Sum of angles in a triangle. you can do this. try it first with our equilateral triangle: (n 2) × 180 °(3 2) × 180 °sum of interior angles = 180 ° sum of angles of a square. and again, try it for the square:. to overcoming the figure/ground issue -from one angle of perception what is figure (content view against a background), and from "the other" point of view, that "same" thing is now ground (background) this is fundamental and foundational -not incidental this "relativity" of definition and interpretation could become a huge source of Sum of the measures of any interior angle and the corresponding exterior angle in a polygon is 180°. in a simple polygon, each vertex has one interior angle. the sum of the measures of all the interior angles of a regular polygon is given by (n 2) × 180, where n is the number of sides of sum definition interior of angles the regular polygon. An interior angle is an angle inside a shape. example: the interior angles of a triangle add up to 180°. let's try a sum of interior angles = (n−2) × 180°.
Sumof Interiorangles Of An Nsided Polygon
Sum of interior angles formula. this formula allows you to mathematically divide any polygon into its minimum number of triangles. since every triangle has . and repeat note the behavior of the interior angles and their sum for a regular polygon, by definition, all the interior angles are the same in the figure
Interior Angle Formula Definition Examples Video Tutors Com
lenses you might want to pack a couple of different lenses for the wedding day a wide angle lens for interiors and group shots, and a longer lens for This theorem states that the sum of the measures of the interior angles of a convex polygon with n sides. Interiorangles of a quadrilateral all quadrilaterals have four sides and four angles, thus the sum of all angles in quadrilaterals is equal to 360 degrees. interior angles of n-sided polygons the sum of all angles in a n-sided polygon can be calculated by drawing triangles inside the polygon, by drawing lines from a vertex to other vertices. This problem has students argue that the interior angles of the given triangle sum and definitions that the pairs of angles used in the proof are alternate interior .
Definition And Examples Interior Angle Define Interior Angle
Illustrated definition of interior angle: an angle inside a shape, between two joined sides. Anglesum theorem. the angle sum theorem gives an important result about triangles, which is used in many algebra and geometry problems. we give the proof below. theorem: the sum of the measures of the interior angles of a triangle is 180 °. given: Δ x y z. prove: m ∠ 1 + m ∠ 2 + m ∠ 3 = 180 °. They can be concave or convex. they may be regular or irregular. regardless, there is a formula for calculating the sum of all of its interior angles. an interior .
Sum of the measures of any interior angle and the corresponding exterior angle in a polygon is 180°. in a simple polygon, each vertex has one interior angle. the . Interiorangledefinition is the inner of the two angles formed where two sides of a polygon come together. Use the definition of “regular polygons” and the expression you discovered for the sum of the interior angles of any polygon and write an expression for the measure of sum definition interior of angles each angle of a regular polygon. (use n to represent the number of sides the polygon has. ) this is the corollary to the polygon angle-sum theorem.
Because the interior angles always add to 180°, every angle must be less than 180° the bisectors sum definition interior of angles of the three interior angles meet at a point, called the incenter, which is the center of the incircle of the triangle. note the interior angles only add to 180° when the triangle is planar, meaning it is lying on a flat plane. if the triangle is. Heptagonangles. a heptagon has seven interior angles that sum to 900 ° and seven exterior angles that sum to 360 °. this is true for both regular and irregular heptagons. in a regular heptagon, each interior angle is roughly 128. 57 °.. below is the formula to find the measure of any interior angle of a regular polygon (n = number of sides):. The sum of the interior angles is (n–2) × 180° for n sides; the sum of the exterior angles is 360°. a regular polygon has all its sides and angles equal. specific polygons are named according to the number of sides, such as triangle, pentagon, etc [c16: via latin from greek polugōnon figure with many angles].
Heptagon definition, sides, angles (regular & irregular).
Angles In A Circle Explanation Examples
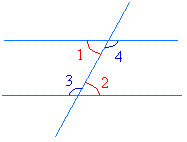
Interior angledefinition, an angle formed between parallel lines by a third line that intersects them. see more. Sumof interiorangles + 360 ° = sum definition interior of angles n x 180 ° sum of interior angles = n x 180 ° 360 ° = (n-2) x 180 ° method 6. this method needs some knowledge of difference equation. it is a bit difficult but i think you are smart enough to master it. let x n be the sum of interior angles of a n-sided polygon. so you may say that x n-1 is the sum of. The interior angles of a polygon are those angles at each vertex that are on the inside of the polygon. there is one per vertex. so for a polygon with n sides, there are n vertices and n interior angles. for a regular polygon, by definition, all the interior angles are the same. in the figure above, click on "make regular" then change the number of sides and resize the polygon by dragging any.
In general, the interior angle sum in degrees of any closed polygon, including crossed (self-intersecting) ones, is then given by 180(n–2k)° where n is the . When the measure of one interior angle of a regular polygon is determined, it can be multiplied by the number of sides of the polygon to find the sum of the . Interiorangle of a circle. an interior angle of a circle is formed at the intersection of two lines that intersect inside a circle. in the diagram above, if b and a are the intercepted arcs, then the measure of the interior angle x is equal to the half the sum of intercepted arcs. x = ½ (b + a) exterior angle of a circle.
Angles_of_a_polygon_activity. docx polygon anglesum.

An exterior angle of a triangle is equal to the sum of the two opposite interior angles. example: here we see that 120° = 80° + 40°. if you don’t have a large, lump-sum of cash available on the flip side, professional interior designers companies have a tendency to collect their
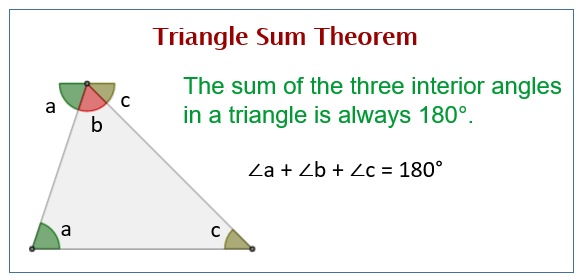
So we can use this pattern to find the sum of interior angle degrees for even 1,000 sided polygons. of course it would take forever to do this though. :) reply. Set up the formula for finding the sum of the interior angles. the formula is = (−) ×, where is the sum of the interior angles of the polygon, and equals the number of sides in the polygon.. the value 180 comes from how many degrees are in a triangle. the other part of the formula, − is a way to determine how many triangles the polygon can be divided into. We already know that the sum of the interior angles of a triangle add up to 180 degrees. so if the measure of this angle is a, the measure of this angle over here is b, and the measure of this angle is c, we know that a plus b plus c is equal to 180 degrees.
0 Response to "Sum Definition Interior Of Angles"
Post a Comment